Quotient math definition

A quotient is the result of performing a division For example if we divide 8. So the quotient is 4. Sometimes, when the division is not exact, the quotient is the integer part of the result. Here, is the quotient and is the remainder.

In math, the definition of quotient is the number which is the result of dividing two numbers. The dividend is the number that is being divide and the divisor is the number that is being used to divide the dividend.

Quotient is the result of a division. English dictionary definition of quotient. The number obtained by dividing one quantity by another. In ÷ = 1 is the quotient.

Il s ’ agit du résultat obtenu suite à la division de deux nombres. La division fait partie des bases de l ’ arithmétique, qu’ il s ’ agisse de division entière ou de division euclidienne. Le nombre est le dividende et le nombre est le diviseur. Dans l’opération « 4÷ = 1», le nombre 1est le quotient.

When you divide bythe number is the example of the quotient. A result obtained by dividing one quantity by another. It makes it somewhat easier to keep track of all of the terms.

A mathematical relation of two trigonometric functions in quotient form with another trigonometric function is called the quotient trigonometric identity. Basic Math Definitions. We have collected some basic definitions on this page. For lots more definitions.

In this lesson, you will learn how to find a quotient using simple division. The quotient is also called the answer! That makes a lot of sense: if you divide one number by a secon you are figuring out "how many times" the second number goes into the first.

Definition Let Fbe a fiel V a vector space over Fand W ⊆ V a subspace of V. For vv∈ V, we say that v≡ vmod W if and only if v− v∈ W. In topology and related areas of mathematics, a quotient space (also called an identification space) is, intuitively speaking, the result of identifying or "gluing together" certain points of a given topological space. The points to be identified are specified by an equivalence relation.

By examining the limits of sums, products and quotients of variable quantities, Mengoli was setting up the basic rules if the calculus thirty years before Newton and Leibniz. Step 1: Name the top term f(x) and the bottom term g(x). You can also call it the result.

The Remainder will always be less than the Divisor. In mathematics, a quotient is the result of division. For example, when dividing bythe quotient iswhile is called the dividen and the divisor. More simply, you can think of the quotient rule as applying to functions that are written out as fractions, where the numerator and the denominator are both themselves functions.

Some problems call for the combined use of differentiation rules: If that last example was confusing, visit the page on the chain rule. It also allows you to simplify complicated algebraic expressions into simple math. Performs division and returns only the integer portion of the division result.

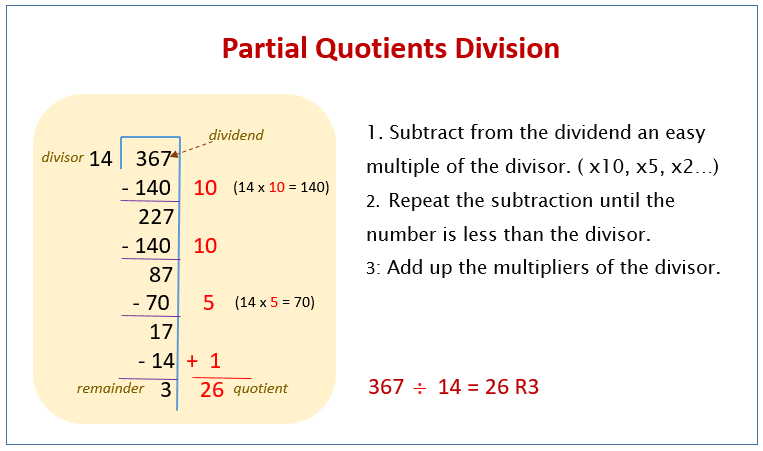
Use this function when you want to discard the remainder of division. Partial quotient is a step-by-step method of division wherein at each step, a partial answer is obtained.

After all the steps have been complete the partial answers are added together to get the quotient. The partial quotient method involves repeated subtraction. The first step is to subtract from the dividend an easy multiple of the divisor. Cours de maths de 6ème.

Des liens pour découvrir. Objectifs du cours: - Savoir écrire un quotient sous forme.

Définition: Le quotient de a par b (où b est un nombre non nul) est le nombre par lequel il faut multiplier b pour obtenir a. Notation: Le quotient de a par b se note.