Contradominio de una funcion radical

Envío gratis con Amazon Prime. Lowest Rates Guaranteed. Hola, te comparto la explicación de este ejercicio de función radical, se trata de hallar el dominio y el rango a la función que muestro en el video. Sea g una función real definida por g(x)=√x.

Contradominio de una función: Son el conjunto de valores que puede tomar la variable dependiente “y”. También es conocido como codominio, recorrido o rango. Tomemos el caso de la función f(x) = 3. Dominio de la función radical de índice impar. El dominio es el dominio de la función radicando.

Cuál es el dominio de la función ? El Contradominio (Codominio, o también conocido como imagen) es el conjunto de llegada, todos los resultados que se pueden escribir de la ecuacion después de asignar todos los valores posibles a x. Y lo que tu mencionas, si aplica ahi. Es cierto que sin importar el valor que le asignes a x, el resultado siempre sera positivo. Están funciones no están definidas para números negativos.

Por lo tanto, el dominio de una funcion radical de indice par sera todos los números reales excepto aquellos que hagan un numero negativo dentro del radical, o tambien lo podemos definir como aquellos valores que hagan igual o mayor que cero el termino dentro del radical. Es importante tener claros estos dos conceptos clave: dominio y codominio de una función algebraica, porque los utilizarás muchas veces y porque ambos son sencillos de entender.

Para ponernos en clima, te invito a repasar lo que compartimos en un post anterior cuando definíamos el concepto de función algbraica. Son funciones polinómicas las rectas, las funciones cuadráticas (parábolas) y las funciones polinómicas de grado superior.

Funciones irracionales son las que vienen expresadas a través de un radical que lleve en su radicando la variable independiente. De hecho, el símbolo radical (como en √x) siempre significa la raíz cuadrada positiva (la principal), así que √x es una función porque su codominio es correcto. Así que el codominio que elijas puede afectar el que algo sea o no una función.

PASOS PARA REPRESENTAR UNA FUNCIÓN RADICAL 1º. La función racional y su dominio. José Enrique Herrera González.

En este trabajo se pretende analizar una función racional a partir de la obtención del dominio considerando los algoritmos más comunes en Cálculo Diferencial asignatura que se cursa en cuarto semestre del bachillerato de nuestra máxima casa de estudios de la Universidad Autónoma del Estado de Hidalgo. Introducción a los números reales.

Si el radical tiene índice impar, entonces el dominio será todo el conjunto R de los números reales porque al elegir cualquier valor de X siempre vamos a poder calcular la raíz de índice impar de la expresión que haya en el radicando. Dado que la plataforma es reciente en nuestro sitio, suponemos que algunos requieren de ayuda para crear una cuenta de usuario.

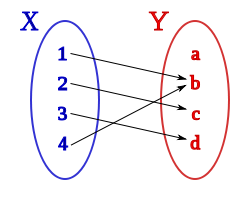
Las funciones radicales son aquellas en las que la variable se encuentra bajo el signo radical. En esta práctica estudiaremos las funciones del tipo y también las que tienen como expresión general.

La gráfica de estas funciones es muy diferente a las de las anteriormente estudiadas. Nota: es importante no confundir la Imagen de una Función con el Codominio de una Función. Nuestra misión es proporcionar una educación gratuita de clase mundial para cualquier persona en cualquier lugar. Khan Academy es una organización sin fines de lucro 501(c)(3).

Una función radical es aquella en la que una expresión que contiene la variable x se encuentra bajo el signo radical. Dado que el dominio de cualquier función polinomial es el conjunto de los números reales, esperamos que el dominio de cualquier función racional sea, excepto aquellos puntos donde el denominador sea cero, es decir, excepto los valores de para los cuales. En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución.

Una regla de correspondencia de una función real de variable real generalmente se da por medio de una o más fórmulas matemáticas y se representa con f (x). Ejemplos explican cómo encontrar el dominio de suma, cociente, composicion de funciones con logaritmos como la raíz de un logaritmo.